Optimized energy scenarios Giudicarie Esteriori

Optimized energy scenarios Giudicarie Esteriori#

Created by Michele Urbani.

In this notebook, we replicate the study in .

Problem description#

Decision variables#

The decision variables are:

  1. PV capacity: the amount of installed PV capacity is 5 MW and it is as the lower bound for the variable, whereas the calculated maximum PV capacity is 42 MW, which is the upper bound.

  2. Heat production technologies: individual wood, oil, LPG boilers, and gound source heat pumps are decision variables expressed as percentages of the total.

  3. Wood organic ranking cycle micro cogeneration provides both thermal and electrical power

Constraints#

The are two constraints: the first concerns the variables at points 2 and 3 of the list above, which must sum to 1. The second constraints limits the total wood consumption to be less than 57 GWh/year.

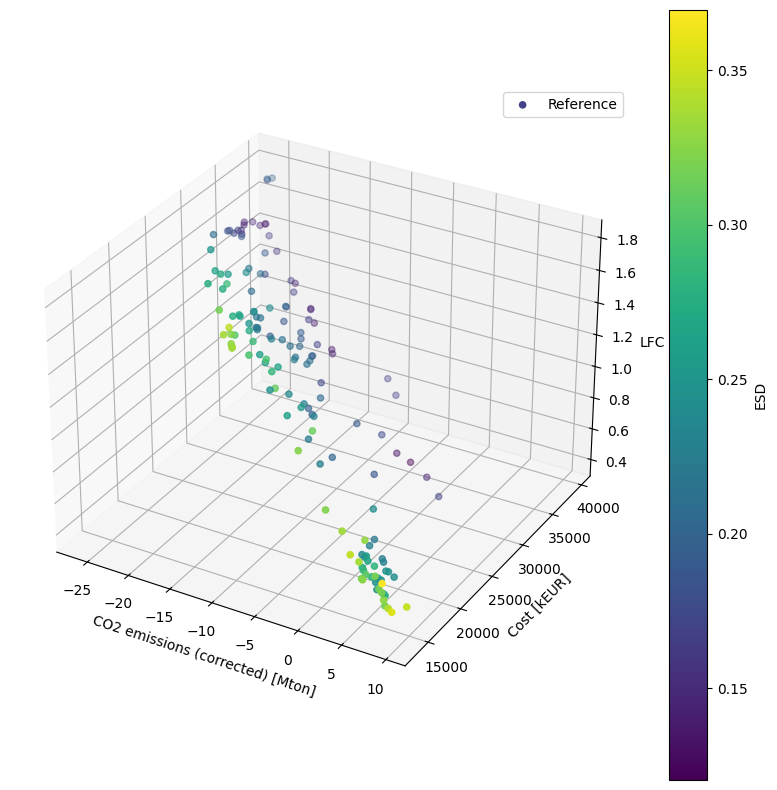
Optimization objectives#

There are four optimization objectives.

  1. CO\(_2\) minimization: the value of produced CO\(_2\) is CO2-emission (corrected) in EnergyPLAN output.

  2. Annual cost minimization: the annual cost is the sum of the annual investment cost, variable operational and maintenance (O&M) cost, fixed operational and maintenacne cost, and the variable O&M and fixed O&M costs.

  3. Load following capacity (LFC) minimization: the LFC expresses how much electricity production follows electrivity demand over a period (yearly in this case).

  4. Energy system dependency (ESD) minimization concerns the reduction of foreign energy import.

Problem declaration#

The _evaluate method is analyzed in the following.

from moea.models import get_model
from moea.algorithms import get_algorithm

model_name = 'Giudicarie'
algorithm_name = 'nsga-ii'

model = get_model(model_name)
algorithm = get_algorithm(algorithm_name, pop_size=100)

2025-08-05 11:30:46.109 | INFO     | moea.config:<module>:11 - PROJ_ROOT path is: C:\Users\murbani\moea

from pymoo.optimize import minimize

res = minimize(
    model,
    algorithm,
    ('n_gen', 20),
    seed=1234,
    verbose=True,
)

Hide code cell output

 
==========================================================================================
n_gen  |  n_eval  | n_nds  |     cv_min    |     cv_avg    |      eps      |   indicator  
==========================================================================================
     1 |      100 |      3 |  0.000000E+00 |  2.858730E+01 |             - |             -
     2 |      200 |      4 |  0.000000E+00 |  1.649660E+01 |  0.3552624049 |         ideal
     3 |      300 |      9 |  0.000000E+00 |  1.146360E+01 |  0.0961991400 |         ideal
     4 |      400 |     12 |  0.000000E+00 |  8.1340000000 |  0.0484775694 |             f
     5 |      500 |     16 |  0.000000E+00 |  6.3120000000 |  0.0890224284 |             f
     6 |      600 |     20 |  0.000000E+00 |  4.9813000000 |  0.0483322873 |             f
     7 |      700 |     22 |  0.000000E+00 |  3.5060000000 |  0.0378091828 |             f
     8 |      800 |     25 |  0.000000E+00 |  2.1549000000 |  0.0384412607 |             f
     9 |      900 |     29 |  0.000000E+00 |  1.3603000000 |  0.1375484273 |         ideal
    10 |     1000 |     32 |  0.000000E+00 |  0.7752000000 |  0.1191417999 |         nadir
    11 |     1100 |     37 |  0.000000E+00 |  0.2903000000 |  0.0293129477 |         ideal
    12 |     1200 |     33 |  0.000000E+00 |  0.000000E+00 |  0.0177090025 |         ideal
    13 |     1300 |     37 |  0.000000E+00 |  0.000000E+00 |  0.0783561236 |         ideal
    14 |     1400 |     40 |  0.000000E+00 |  0.000000E+00 |  0.0112778117 |             f
    15 |     1500 |     38 |  0.000000E+00 |  0.000000E+00 |  0.0291398458 |         ideal
    16 |     1600 |     43 |  0.000000E+00 |  0.000000E+00 |  0.0190765816 |             f
    17 |     1700 |     48 |  0.000000E+00 |  0.000000E+00 |  0.0436931819 |         ideal
    18 |     1800 |     55 |  0.000000E+00 |  0.000000E+00 |  0.0153563429 |             f
    19 |     1900 |     56 |  0.000000E+00 |  0.000000E+00 |  0.0022993929 |             f
    20 |     2000 |     57 |  0.000000E+00 |  0.000000E+00 |  0.0739566735 |         nadir
    21 |     2100 |     58 |  0.000000E+00 |  0.000000E+00 |  0.0018151609 |             f
    22 |     2200 |     54 |  0.000000E+00 |  0.000000E+00 |  0.1415977096 |         ideal
    23 |     2300 |     54 |  0.000000E+00 |  0.000000E+00 |  0.0043143086 |             f
    24 |     2400 |     57 |  0.000000E+00 |  0.000000E+00 |  0.1269304366 |         nadir
    25 |     2500 |     62 |  0.000000E+00 |  0.000000E+00 |  0.0066303390 |         ideal
    26 |     2600 |     63 |  0.000000E+00 |  0.000000E+00 |  0.0635244915 |         ideal
    27 |     2700 |     66 |  0.000000E+00 |  0.000000E+00 |  0.0065035809 |             f
    28 |     2800 |     66 |  0.000000E+00 |  0.000000E+00 |  0.0032630202 |             f
    29 |     2900 |     68 |  0.000000E+00 |  0.000000E+00 |  0.0828845031 |         nadir
    30 |     3000 |     68 |  0.000000E+00 |  0.000000E+00 |  0.0121824457 |         nadir
    31 |     3100 |     72 |  0.000000E+00 |  0.000000E+00 |  0.0063933243 |             f
    32 |     3200 |     74 |  0.000000E+00 |  0.000000E+00 |  0.0338385111 |         ideal
    33 |     3300 |     76 |  0.000000E+00 |  0.000000E+00 |  0.0030370655 |             f
    34 |     3400 |     80 |  0.000000E+00 |  0.000000E+00 |  0.0936090494 |         nadir
    35 |     3500 |     82 |  0.000000E+00 |  0.000000E+00 |  0.0018662569 |             f
    36 |     3600 |     85 |  0.000000E+00 |  0.000000E+00 |  0.0215401698 |         nadir
    37 |     3700 |     88 |  0.000000E+00 |  0.000000E+00 |  0.0030154604 |             f
    38 |     3800 |     91 |  0.000000E+00 |  0.000000E+00 |  0.0014404805 |             f
    39 |     3900 |     91 |  0.000000E+00 |  0.000000E+00 |  0.0014404805 |             f
    40 |     4000 |     92 |  0.000000E+00 |  0.000000E+00 |  0.0022239877 |             f
    41 |     4100 |     92 |  0.000000E+00 |  0.000000E+00 |  0.0030115693 |             f
    42 |     4200 |     93 |  0.000000E+00 |  0.000000E+00 |  0.0001717173 |             f
    43 |     4300 |     94 |  0.000000E+00 |  0.000000E+00 |  0.0289100189 |         ideal
    44 |     4400 |     97 |  0.000000E+00 |  0.000000E+00 |  0.0068740453 |         ideal
    45 |     4500 |     98 |  0.000000E+00 |  0.000000E+00 |  0.0005355608 |             f
    46 |     4600 |     98 |  0.000000E+00 |  0.000000E+00 |  0.0005355608 |             f
    47 |     4700 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0019075056 |             f
    48 |     4800 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0034581768 |             f
    49 |     4900 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0007732338 |             f
    50 |     5000 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0024444155 |             f
    51 |     5100 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0042405858 |             f
    52 |     5200 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0009037632 |             f
    53 |     5300 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0009037632 |             f
    54 |     5400 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0047300319 |             f
    55 |     5500 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0005427791 |             f
    56 |     5600 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0013624404 |             f
    57 |     5700 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0026811135 |             f
    58 |     5800 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0007947801 |             f
    59 |     5900 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0007947801 |             f
    60 |     6000 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0046588147 |             f
    61 |     6100 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0015234393 |             f
    62 |     6200 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0060813605 |         ideal
    63 |     6300 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0017661701 |             f
    64 |     6400 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0017661701 |             f
    65 |     6500 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0025688800 |             f
    66 |     6600 |    100 |  0.000000E+00 |  0.000000E+00 |  0.000000E+00 |             f
    67 |     6700 |    100 |  0.000000E+00 |  0.000000E+00 |  0.000000E+00 |             f
    68 |     6800 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0005073179 |             f
    69 |     6900 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0005073179 |             f
    70 |     7000 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0012420452 |             f
    71 |     7100 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0022084658 |             f
    72 |     7200 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0034385588 |             f
    73 |     7300 |    100 |  0.000000E+00 |  0.000000E+00 |  0.000000E+00 |             f
    74 |     7400 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0005617363 |             f
    75 |     7500 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0006890537 |             f
    76 |     7600 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0006890537 |             f
    77 |     7700 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0006890537 |             f
    78 |     7800 |     99 |  0.000000E+00 |  0.000000E+00 |  0.0028546566 |             f
    79 |     7900 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0179338561 |         ideal
    80 |     8000 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0004894304 |             f
    81 |     8100 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0012335465 |             f
    82 |     8200 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0031946710 |         ideal
    83 |     8300 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0003906560 |             f
    84 |     8400 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0003906560 |             f
    85 |     8500 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010319648 |             f
    86 |     8600 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010319648 |             f
    87 |     8700 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010319648 |             f
    88 |     8800 |     99 |  0.000000E+00 |  0.000000E+00 |  0.0015746528 |             f
    89 |     8900 |     99 |  0.000000E+00 |  0.000000E+00 |  0.0020728633 |             f
    90 |     9000 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0028910149 |             f
    91 |     9100 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0007011033 |             f
    92 |     9200 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010852210 |             f
    93 |     9300 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010852210 |             f
    94 |     9400 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010852210 |             f
    95 |     9500 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010852210 |             f
    96 |     9600 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010852210 |             f
    97 |     9700 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0010852210 |             f
    98 |     9800 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0020574463 |             f
    99 |     9900 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0026504594 |             f
   100 |    10000 |    100 |  0.000000E+00 |  0.000000E+00 |  0.0004154629 |             f

Results analysis#

import pandas as pd
import matplotlib.pyplot as plt

# Load reference data from the paper, no index column and space separated
ref = pd.read_csv('giudicarie-reference.csv', sep=' ', header=None,
                  names=['CO2 emissions (corrected) [Mton]', 'Cost [kEUR]',
                         'LFC', 'ESD'],
                  index_col=False)

# 3D scatter plot
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')

# Use a colormap to set the marker colors
sc = ax.scatter(
    ref['CO2 emissions (corrected) [Mton]'],
    ref['Cost [kEUR]'],
    ref['LFC'],
    c=ref['ESD'],
    cmap='viridis',
    label='Reference'
)

# Add color bar which maps the colors to the ESD values
cbar = fig.colorbar(sc)
cbar.set_label('ESD')

ax.set_xlabel('CO2 emissions (corrected) [Mton]')
ax.set_ylabel('Cost [kEUR]')
ax.set_zlabel('LFC')
plt.legend()
plt.show()
../_images/2c17ad21119dfc22db562392753ed7d4e497350264312b4a1dd477d852ea8b5d.png 
# 3D scatter plot
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')

# Cast results to DataFrame
df = pd.DataFrame(
    res.F,
    columns=[
        'CO2 emissions (corrected) [Mton]',
        'Cost [kEUR]',
        'LFC',
        'ESD'
    ]
)

# Use a colormap to set the marker colors
sc = ax.scatter(
    df['CO2 emissions (corrected) [Mton]'],
    df['Cost [kEUR]'],
    df['LFC'],
    c=df['ESD'],
    cmap='viridis',
    label='Reference'
)

# Add color bar which maps the colors to the ESD values
cbar = fig.colorbar(sc)
cbar.set_label('ESD')

ax.set_xlabel('CO2 emissions (corrected) [Mton]')
ax.set_ylabel('Cost [kEUR]')
ax.set_zlabel('LFC')
plt.legend()
plt.show()
../_images/83d4db49be143eee180e366efba52f4bf3f2d93d9c8e137b5c8e270e3959c9b5.png

Convergence analysis#

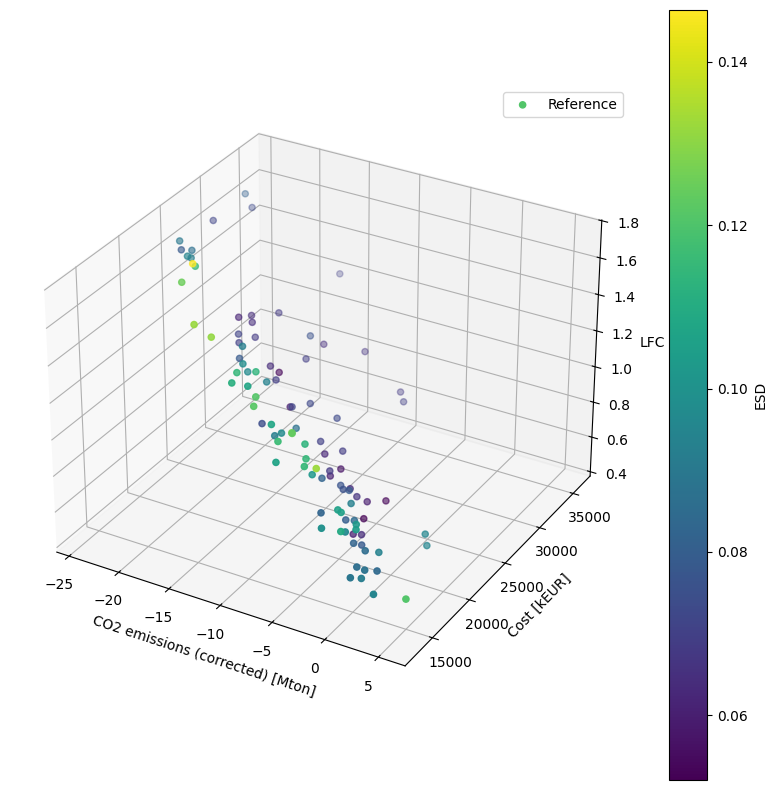
The results of the paper are used as reference to measure the quality of the solution. We implement the Inverted Generational Distance (IGD) to quantify the distance from any point in the set of solutions \(Z\) to the closest point in the set of reference solutions \(A\).

\[ IGD(A) = \frac{1}{|Z|} \left( \sum_{i=1}^{|Z|} \hat{d}_i ^{\,p} \right) ^{1/p} \]

where \(\hat{d}_i\) represents the Euclidean distance (\(p=2\)) from \(z_i\) to its nearest reference point in \(A\).

The lower the value of the IGD, the closer the set \(A\) to the reference set \(Z\).

from pymoo.indicators.igd import IGD

ind = IGD(ref.values)
print("IGD", ind(res.F))

IGD 281.20622479628685

References#

Contents